\(为什么0.9999\cdots=1\)

有不少人不能理解为什么无限循环小数\(0.9999\cdots=1\)，而认为\(0.9999\cdots<1\)。理由如下：0.9小于1，0.99小于1，\(0.9\cdots9\)(小数点后无论有多少个9)也都小于1，这样，即使小数点后有无穷多个9，无限循环小数\(0.9999\cdots\)还应该小于1，而不应该等于1。

这看上去似乎有些道理，但其实是一种误解，是由于没有理解无限循环小数的确切含义造成的。事实上，有一些巧妙的“证明”立即可以说明无限循环小数\(0.9999\cdots=1\)。比如，

无限循环小数

证法1：设\(x=0.9999\cdots\)，那么， \[10x=9.9999\cdots=9+0.9999\cdots=9+x.\] 这样，\(10x–x=9\)，即可求得\(x=1\)。

证法2：我们已经知道\(1/3=0.3333\cdots\)，等式两边同乘以3，立即得到\(1=0.9999\cdots\)。

这样的“证明”有很多，读者也可以想出自己的方法来。上述的证法1特别有意思，它不仅告诉我们\(0.9999\cdots=1\)，而且还给出了化无限循环小数为分数的一个方法。

不过，有读者可能会说：上面的证明我认可，可是我还是觉得\(0.9999\cdots\)要比1小，这样的证明并没有消除我原有的疑惑，也不明白为什么\(1/3=0.3333\cdots\)。

几种著名的极限

为此，现在让我们详细解释为什么\(1/3=0.3333\cdots\)。从这个解释中会看到一个无限循环小数是怎样形成的，正确理解无限循环小数的意义，特别是能看到它与有限小数的区别，从而最终消除大家的疑惑。现在让我们先看一看下列用3去除1的算式：这里，我们每做一次除以3（即除式顶部每添加一个3），都用了一次\(10–3×3=1\)或\(10÷3=3\cdots1\)。正因为每次除以3都余1，使得除以3这个过程可以无限重复地做下去，从而得到的商是一个无限循环小数\(0.3333\cdots\)，这样我们就有了\(1/3=0.3333\cdots\)。

如果我们仅做有限次除以3，即上面的竖式只是一个有限竖式，那么，竖式的下端总有一个余数1，这是我们能继续除下去的基础，同时也说明了\(0.33\cdots3\)(有限个3)是小于\(1/3\)的。但是，我们在做了无限次除以3，即左面的竖式变为一个无限长的竖式后，把最右下端的1给忽略掉了，而直接让\(1/3=0.3333\cdots\)。那么，为什么此时这个1消失了，或者说扔掉这个1是合理的呢？我们来看看每次除以3所余的1到底是什么。

如果只除以3一次，竖式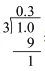表示的是\(1/3=0.3+0.1/3=0.3+(1/3)×10^{–1}\)，而竖式中最下面的余数1表示的是余项\((1/3)×10^{–1}\)。如果除以两次3，意味着\(1/3=0.33+0.01/3=0.33+(1/3)×10^{–2}\)，余数1表示\((1/3)×10^{–2}\)。一般地，除n次得到 \[1/3=0.\underbrace{ 33\cdots3 }_{\text{ \(n\)个}3}+(1/3)\times10^{-n}.\] 余数1表示的是\((1/3)×10^{–n}\)。这时，我们将1/3分成了两个部分之和，第一部分是小数\(0.33\cdots3\)，第二部分是余项\((1/3)×10^{–n}\)。现在如果除无限次，即除的次数\(n\)等于无穷大，那么，第一部分的小数就变成了无限循环小数\(0.3333\cdots\)，而第二部分余项呢？我们立刻可以看到，它变成了0！现在明白了，原来我们用竖式做除法，除无限次后扔掉的其实不是1而是0，当然可以把它忽略掉了。而式子 \[1/3=0.\underbrace{ 33\cdots3 }_{\text{ \(n\)个}3}+(1/3)\times10^{-n}.\] 就变成了\(1/3=0.333\cdots+0=0.3333\cdots\)

由于次数\(n\)是一个数，而无穷大不是数，说“\(n\)等于无穷大”并不准确，数学上我们说\(n\)趋向于无穷大，记为\(n→∞\)。此时，余项\((1/3)×10^{–n}\)趋向于0，而小数\(0.\underbrace{ 33\cdots3 }_{\text{ \(n\)个}3}\)趋向于无限循环小数\(0.3333\cdots\)，分别记为\((1/3)×10^{–n}→0\)和\(0.\underbrace{ 33\cdots3 }_{\text{ \(n\)个}3}→0.3333\cdots\)。我们把上述过程列一个表可以看得很明白：

\[1/3\]	\[=\]	\[0.3\]	\[+ \quad (1/3) ×10^{-1}\]
\[1/3\]	\[=\]	\[0.33\]	\[+ \quad (1/3) ×10^{-2}\]
\[\vdots\]	\[\]	\[\vdots\]	\[\vdots\]
\[1/3\]	\[=\]	\[0.33\cdots3(n个3)\]	\[+ \quad (1/3) ×10^{-n}\]
\[\downarrow\]	\[(n \rightarrow \infty)\]	\[\downarrow\]	\[\downarrow\]
\[1/3\]	\[=\]	\[0.3333\cdots\]	\[+ \quad \quad \quad 0 \quad \quad \quad\]

上述过程表明：不管小数点后有多少个3，只要是有限多个，\(0.33\cdots3\)总小于\(1/3\)，但一旦小数点后有了无限多个3，\(0.3333\cdots\)却是实实在在等于\(1/3\)！这一事实也说明，我们不能把对任意“有限”的情形成立的事实，简单地搬到“无限”的情形。一旦涉及无限，情况就会变得很奇特。

现在回来说明\(1=0.9999\cdots\)就相对比较容易了，我们也只要列一个类似的表就能完全说明问题了。

\[\quad 1\]	\[=\]	\[\quad \quad \quad\ 0.9\quad \quad \quad \quad\]	\[+ \quad \quad \quad 10^{-1}\]
\[\quad 1\]	\[=\]	\[0.99\]	\[+ \quad \quad \quad 10^{-2}\]
\[\quad \vdots\]	\[\]	\[\vdots\]	\[\quad \quad \quad \vdots\]
\[\quad 1\]	\[=\]	\[\quad \quad \quad \quad \quad 0.99\cdots9(n个9)\]	\[+ \quad \quad \quad 10^{-n}\]
\[\quad \downarrow\]	\[\quad (n \rightarrow \infty)\]	\[\downarrow\]	\[\quad \quad \quad\downarrow\]
\[\quad 1\]	\[=\]	\[\quad \quad \quad 0.9999\cdots\]	\[\quad \quad + \quad \quad \quad 0 \quad \quad \quad\]

影响人们承认\(0.9999\cdots=1\)的原因，可能是将对任意有限的小数成立的事\(0.99\cdots9\)小于1，想当然地照搬到无限循环小数\(0.9999\cdots\)上了。

顺便指出，每个有限小数都有一个无限循环小数和它相等，比如\(0.25=0.249 999\cdots\)。因此，分数化为小数时有时并不唯一，但每个分数都可化为无限循环小数，且是唯一的。