任何三角形都等腰？听到这样的结论，人们的第一反应是：这绝不可能。不相信吗？看看我们给出的“证明”。

如果三角形本来等腰，结论自然成立。下面给出非等腰三角形也等腰的“证明”。

证明过程是这样的。设三角形\(ABC\)是非等腰三角形。我们分别作出\(∠A\)的平分线与\(BC\)边的垂直平分线，则两者一定相交（若重合或平行，都会推出三角形等腰）。

设交点为\(O\)点，则两者或相交于三角形内部，如图1所示；或相交于三角形外部，如图2所示。

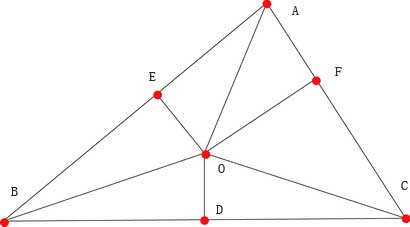图1

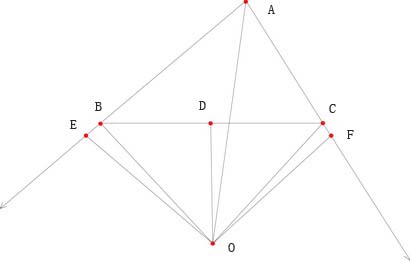图2

过点\(O\)分别作\(AB\)、\(AC\)的垂线\(OE\)与\(OF\)，交\(AB\)于点\(E\)，交\(AC\)于点\(F\)，两个直角三角形\(AOE\)与\(AOF\)有一公共边\(AO\)，又\(∠EAO\)=\(∠FAO\)，因此两三角形全等。由此推得\(AE\)=\(AF\)，并且\(OE\)=\(OF\)。

连接\(OB\)、\(OC\)，因为\(OB\)=\(OC\)（\(O\)为\(BC\)垂直平分线上的点），所以直角三角形\(OBE\)与直角三角形\(OCF\)全等，从而\(BE\)=\(CF\)。

于是，对图1情形有\(AB=AE+BE=AF+CF=AC\)。而对图2情形有：\(AB=AE–BE=AF–CF=AC\)。

无论哪种情况，我们都证明了非等腰三角形\(ABC\)等腰！

“证明”似乎无懈可击，结论却明显不成立。问题出在什么地方呢？“证明”过程中的漏洞点出来其实很简单：上面画的图形是不准确的。正确的图形如图3所示（设\(AB\)>\(AC\)）：

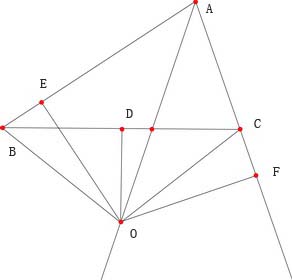图3

这样，虽然如上面所证，仍能通过两个三角形全等推得\(AE=AF\)以及\(BE=CF\)。但\(AB=AE+BE\)，而\(AC=AF–CF\)，因此推不出\(AB=AC\)。

这一方面提醒我们，画图时应注意准确，否则会把自己引入歧途。另一方面告诉我们直观尽管有很大用处，但是由几何直观得到的结论并不一定可靠。