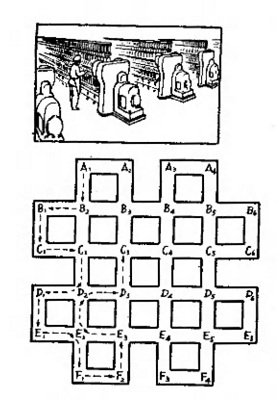
在纺织工厂里，纺织女工在车间来回地操作，每天要来回走很多趟，如果她所负责的区域如左下图，你看，她能不能从任意一点出发，不重复地走过所有的走道，而最后又回到出发点？

这个问题的解决并不难，它可以归结为一种古老的数学游戏——“一笔画”的问题。什么是“一笔画”呢？就是由某些点和线段所组成的各种图形，问这些图形能不能不重复地—笔画成。

后页上的图形都可以一笔画成。

再看看下图的任意两点，都可以用若干线段把它们连结起来，这样的图形称为连通的。这种图形中的许多点，可以分成两类：凡是从这个点出发的线段的数目是奇数的，称为奇点（如右图中的A点和B点），如果从这个点出发的线段的数目是偶数的，称为偶点（如图中的C、D、E、F、G、H各点）。从各式各样的这类图形看来，我们可以知道，凡是能够一笔画成的图形，只有两种情况：

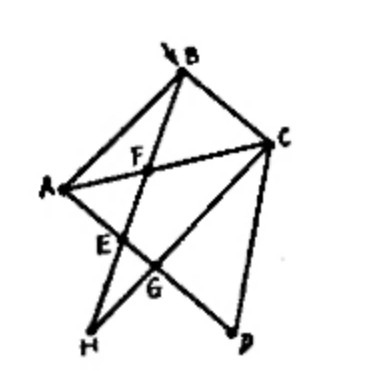1.图形中的所有的点都是偶点，就可以从图形的任意一点出发，不重复地把图形一笔画出，而且最后仍回到出发点。

2.图形中只有两个奇点的，这时，可以从其中一个奇点出发，把图形不重复地一笔画出，最后回到另一个奇点。

如果图形中奇点的个数多于两个，就不可能把图形不重复地一笔画出。

为什么这两种图形可以一笔画出呢？

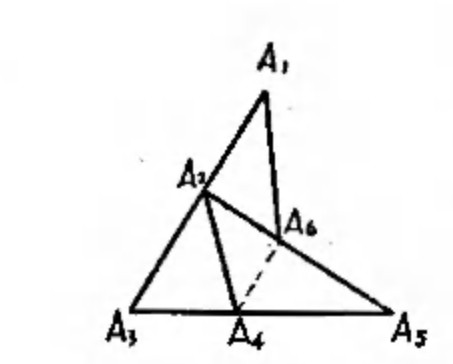
我们先来看第一种情况，图形是连通的，而且没有奇点，如后面的第一个图就是这样的图形。从这个图形的任意一点出发，可以划一条闭回路出来，最后还是回到出发点。例如，从A₁出发，经A₂、A₅、A₆最后回到A₁（如图上虚线划出的部分）。现在我们把这一部分擦去，留下的部分如右下图所示，这个图形仍旧只有偶点而没有奇点。因此，它也可象上面一样找到闭回路，例如找出A₆、A₇、A₃、A₆这一条闭回路。又因为A₆这一点在原来的闭回路中也是有的，因此，可以把后面一条闭回路接到前面一条闭回路中去，得到这样一条大的闭回路：A₁、A₂、A₅、A₆、A₇、A₃、A₆、A₁（画出来的部分就是接上去的闭回路）。下面就可把这一条闭回路擦去，又在留下的部分中找闭回路，再接到上面的闭回路中。这样下去，可以把整个图形接成一条闭回路，也就是可以把图形一笔画出，而且出发点和终点是一致的。

现在就能很容易地说明第二种情况了。即图形是连通的，而且只有两个奇点。如下图，只有A₄、A₆两个点是奇点，其余点都是偶点。我们只要在两个奇点之间添一条线，它们也都变成了偶点，这就成了第一种情况了。于是可以把这个图形一笔画出，并且假设第一笔画的就是添上去的那根虚线。如在图上的情形是：A₆、A₄、A₂、A₁、A₆、A₅、A₄、A₃、A₂、A₆。再把第一笔去掉，就把原来的图形一笔画出了：A、A₂A₁、A₆、A₅、A4、A₃、A₂、A₆。

到这里，我们可以很容易地解决开头提出来的一问题了。因为车间走道所成的图形是连通的，而且交叉点全是偶点，因此，要不重复地走过所有走道，而最后回到出发点是可能的。其中的一种走法是：

A₁、B₂、B₁、C₁、C₂、D₂、D₁、E₁、E₂、F₁、F₂、E₃、E₂、D₂D₃、C₃、C₂、B₂、B₃、C₃、C₄、D₄、D₃、E₃、E₄、F₃、F₄、E₅、E₄、D₄、D₅、D₆、E₆、E₅、D₅、C₅、C₄、B₄、B₅、B₆、C₆、C₅、B₅、A₄、A₃、B₄、B₃、A₂、A₁。

其实，还有很多种走法，你不妨试一试。