平面几何告诉我们，“三角形的内角之和等于180°”。由于这是一条被证明了的定理，因而对于“三角形内角之和会不会不等于180°”这样一个“怪”问题，就恐怕很少会有人去设想了。

其实，它倒真是个问题。早在100多年前，或者更早的时候，已经有人设想了，不仅设想和研究了这个问题，而且还得出并证明了如下两个截然相反的结论：

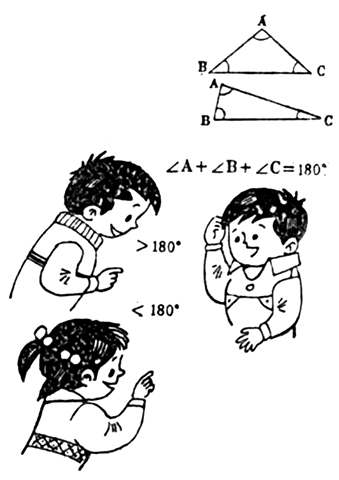
“三角形内角之和大于180°。”

“三角形内角之和小于180°。”

这不是在开玩笑吗！怎么能够让三个彼此矛盾的命题同时为真呢？又怎么可能竟然都被证明为真呢？但这毕竟是事实。下面说说这究竟是怎么一回事。

我们知道，数学中的证明通常是用演绎推理来进行的，即用已知的或者说已被证明了的定理作前提来推断所要证明的命题的正确性。既然每一个数学命题的证明都需要用巳被证明的命题作前提，那么，数学的证明过程将是一种无限往回追溯的不可能完成的事了，除非人们允许追溯到某一步可以停止。这样，也就不得不选用一些公认成立而不再要求证明的命题（它们被称之为公理或公设），从这些公理或公设出发，通过纯逻辑的推理（即演绎推理），来导出所有其他的定理。

比如，选用来推出中学平面几何中的定理的公理和公设分别有5条，它们是：

公理1：与同一个量相等的两个量相等；

公理2：等量加等量，其和相等；

公理3：等量减等量，其差相等；

公理4：彼此重合的图形全等；

公理5：全部大于它的部分。

公设1：从任意一点到另一点可以引直线；

公设2：直线可以无限地延长；

公设3：以任意一点为圆心，可以用任意长度的线段作半径画圆；

公设所有的直角都相等；

公设5：如果两条直线与另一条直线相交，所成的同侧内角的和小于两直角，那么这两条直线在这一侧必相交。

公理和公设的选取当然要求满足一定的条件。例如，它们相互之间不能矛盾，而由它们导出的定理也不能有相互矛盾之处；它们要尽可能地少些，而却又能由它们导出这个命题系统中的所有的定理；它们彼此之间又是互相独立的，你推导不出他，他也推导不出你。当然，公理和公设的语句最好简洁明瞭，使人愿意承认它。

用这样的标准去对照上面所列出的公理和公设，可以发现，除了公设5以外，它们所反映的都只是有限范围内的情况，因此可以用实验来加以验证，从而使人承认它的真实性。但是，公设5却不是这样。由于对它的真实性的确认涉及到无限大的范围，这是无法用实验来验证的，因此从公元4世纪起，这条公设便被多次怀疑了。数学家认为它缺乏作为几何学公设应该具有的使人相信其真实的品性。于是，数学家纷纷用其他几条公理和公设去证明它。倘若成功了，那就说明它没有资格作为公理。倘若不成功，那人们对它作为公理也就放心些了。

可是，经过1000多年断断续续的努力，数学家们虽然没有能够成功地证明出第5公设，但却发现了许多有趣的事实。事实之一是，第5公设与“三角形内角之和等于180°”这个命题是等价的。所谓命题等价是指它们之间可以相互推得。事实之二是，如果第5公设被否定，也就是说用一个与第5公设对立的命题，例如，“三角形内角之和小于180°”，或者“三角形内角之和大于180°”来代替它，那么，由其他5条公理和4条公设，再加上这条第5公设的对立命题所推导出来的所有命题，都被证明是正确的，即它们之间都没有逻辑矛盾。这说明，人们完全可以把与第5公设无关的，以及与第5公设对立的命题，组建成另一种几何学。这种几何学中的命题虽然与我们的经验不一致，但它们都是经过证明的“真理”。

经过这样一番说明以后，我们就不难了解：“三角形内角之和等于180°”与“三角形内角之和大于180°”或“三角形内角之和小于180°”的真理性是等同的，因为它们都可以在某种几何学中得到证明。问题是“三角形内角之和等于180°”与我们的经验相吻合，容易被人们所接受，而其他两条定理与我们的经验不相吻合，比较陌生而已。但是，要知道，真理是不以经验来确认的。确认真理需要的是理性，是逻辑法则。

数学上把确认三角形内角之和等于180°的几何叫做.“欧几里得几何”，简称“欧氏几何”，而把确认三角内角之和不等于（包括大于或小于）180°的几何叫做“非欧几何”。19世纪，非欧几何分别由俄国的罗巴切夫斯基和德国的黎曼创立，前者创立的称为罗氏几何，后者创立的称为黎曼几何。20世纪初，非欧几何开始应用于力学和物理学。特别是1915年爱因斯坦把非欧几何应用到了他的广义相对论上，这不仅进一步加深了人们对非欧几何的认识，而且促使了它继续发展。