现在有式样、大小完全相同的四张硬纸片，上面分别写了1、2、3、4四个不同的数字。如果不看数字，任意抽一张，取出来的那一张是什么数字呢？

不一定，1、2、3、4都是可能的。因为它们的式样、大小完全相同。我们又是任意抽取的。应该说，1、2、3、4这几个数字被抽出的机会完全均等。所以，每一个数字被抽取的机会都是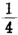。这是理论。实践怎样呢？如果你这样试抽比较多的次数，譬如说一万次，那么，我们会发现，1、2、3、4被抽取的次数，大致都接近于2500次，即都接近于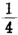的次数。实践和理论是一致的。抽取的次数越多，这个数字可以越接近。

在数学里，我们把一件事情可能发生的次数，在实践的总次数中的那个比值，叫做这件事情发生的概率。

这里，在每一次抽取中，抽出的数字是1、2、3或4的概率都是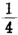。而它们的总和是1。

让我们把问题再搞复杂一点。

如果在每次抽取中同时抽出两张，把两张的数字加起来，那么，这两个数字的和等于5的概率是多少呢？

这里，总共可以有5种结果，即它们的和是3、4、5、6或7。那么，是不是它们的概率都是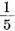呢？

不是的，因为它们的机会不是均等的。

这里，一共有6种可能：

1+2=3，1+3=4，1+4=5，

2+3=5，2+4=6，3+4=7。

这六种是机会均等的。其中有二种不同情况1+4和2+3结果都是5。

因此，我们说，和是5的概率应该是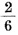即。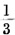

大量实践后的统计结果证明，这样的估计也是符合实际的理论。

我们再搞得复杂一点。

如果连续抽取两次，每次只抽一张，抽后仍旧放还。这样连抽二次都抽到2字的概率是多少呢？

我们可以这样分析。如果实践4000次。因为1、2、3、4是机会均等的。结果是抽到2字的次数是接近1000次的。在第一次抽不到2的3000次中第二次抽取时，不论再抽到什么，都不符合要求。第一次抽到2的1000次中，第二次又抽到2的应该接近1000的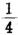，即250次。所以连续两次都抽到2的概率应该是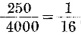。即。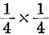

当然，不要忘记，这叫概率，在具体实践中，是接近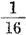，不能要求一点点也没有相差的。

概率的计算对我们的日常生活有没有用处呢？有的。譬如在大量生产某种产品时，要抽样检验，估计废品率；譬如，在高炮部队炮打敢于侵犯我国领空的敌机时，要计算命中率等等，都要用到概率的计算。

因为概率的计算有许多重要的用处，所以已经发展成为数学的一门分支，叫做“概率论”。