1980年，上海博物馆考古部在清理明代古墓的出土文物时，发现了一块元代穆斯林所佩戴的玉挂。所谓“玉挂”，实际上与《红楼梦》中贾宝玉所佩戴的“通灵宝玉”是同一类东西。它的发现，对研究古代中国与阿拉伯各国的文化交流、阿拉伯数字的演变历史以及穆斯林的风俗习惯，都提供了不少重要资料。

这块玉挂的背面是一个四阶幻方，由16个古阿拉伯数目字组成。这些古代阿拉伯数字和现在常见的1，2，3…等完全不一样，如果你们看到的话，可能一个都不认识。经专家研究，这个幻方中的数字如左图所示。

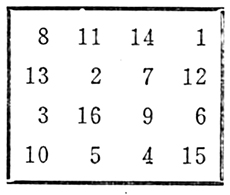这是一个很奇妙的幻方。它除了具有由1到16的16个连续自然数所组成，既无重复，也不遗漏，以及任何一条横行、纵列或对角线上的四个数字之和都等于34这两项一般四阶幻方都含有的通性以外，还具有如下的一些特异性质：

（1）任何一条“折断”的对角线上的四个数字之和也都等于34。例如：

14+12+3十5=34；

5+9+12+8=34；

……

（请一面看图，一面看等式，进行对照）

怎样寻找“折断”的对角线呢？我们假定幻方可以在上、下、左、右无限重复，如下图所示：

在图上任意用笔画一条包含四个数字的直线（纵、横、斜的直线都可以），那么线上的四个数字之和都将等于34。

上述这一特性是任何三阶幻方所没有的。凡是具备这种性质的幻方就称为“完全幻方”，也叫“仙灵幻方”、“恶魔幻方”等。仙灵也好，恶魔也好，无非说明它的奇异而已。幻方研究家们指出，阶数4已经是最小的下限。阶数更低的完全幻方就不存在了。

（2）这个幻方中的任何一个二阶子幻方的四个数字之和均等于34。例如：2+7+9+16=34。

（3）这个幻方中的任何一个三阶子幻方的角上四个数字之和也等于34。例如：2+12+15+5=34。

（4）假如将这个幻方看成象棋盘来飞“象”，那么不管你从哪一点出发，飞到哪一点，这两小点上的数字之和都等于17。例如：13+4=17。

如果你再深入研究一下这个幻方，或许还会有一些新的发现哩！