《十万个为什么》数学第1册里，介绍过我国古算书中的一些著名的数学问题——“百鸡问题”等。在四五世纪的数学著作《孙子算经》里，还有一个数学问题也很著名，其内容是：

“今有雉（鸡）兔同笼，上有三十五头，下有九十四足。问雄兔各几何。”

后人称这类问题为鸡兔同笼问题。

用现在列方程解应用题的方法，这个问题很容易解决。设鸡有x只，兔有y只，则根据题意有：

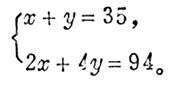
解之得x=23，y=12。

《孙子算经》用的是算术方法：脚数的一半减头数，即$\frac{{94}}{2} - 35 = 12$为兔数；头数减兔数即35-12=23为鸡数。这一解法直接而自然，也很合乎逻辑。书中没有注明这样解法的原因，但其思路是不难设想的。

因为鸡有2只脚，兔有4只脚，取脚数的一半后，就鸡而言，其头数与脚数就一致了。于是一半的脚数与头数的差，就该是兔的只数。总头数减去兔的只数，自然就是鸡的只数。

将上述思路用符号表示出来，就更清楚了。设鸡有x只，兔有y只，那么一半脚数减头数就是$\frac{1}{2}\left( {2x + 4y} \right) - \left( {x + y} \right) = y$；头数减去兔的只数就是（x+y）-y=x。

鸡兔同笼问题后来有许多变化，解法也各有不同。上面这道题另有一种解法是，先设全部是兔，则总足数是头数的4倍，得140。与实际足数相减，即140-94，得误把鸡当兔时多计算的足数46。每只多算2足，故折半即为鸡数23。总头数减鸡数为兔的只数12。

鸡兔同笼问题不仅有趣，而且直觉性较强，对培养初学算术四则应用题的学生的逻辑推理能力和运算技巧很有帮助，因而历代算书多有引录，国外也很有影响。