什么样的正多边形可以用尺规作图
用直尺和圆规,容易作出正三角形、正六边形和正方形。多花点心思的话,正五边形也能画出来。但要用尺规作图作出其他正多边形,似乎不太容易。正七边形能否用尺规作图作出,这个问题曾经难倒过不少几何学家。我们不禁要问,什么样的正多边形能用尺规作图画出来?
 |  |
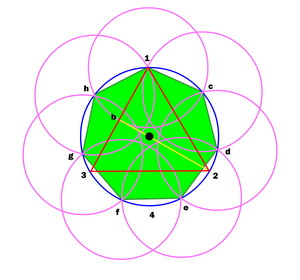 |
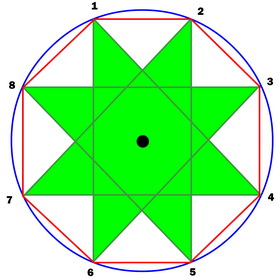
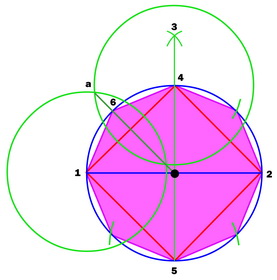
| 几个尺规作图的实例 |
第一位给这个问题带来曙光的,是大数学家高斯。他在年仅19岁的时候,就证明了正十七边形能用尺规作图,这是正多边形的尺规作图从古希腊以来的第一个突破。而在仅仅五年之后,他在著作《算术研究》中,就给出了如下的定理:假设\(n\)是一个整数,如果\(n\)是2的幂和几个不同的费马素数的乘积,那么正\(n\)边形可以用尺规作图作出。所谓费马素数,就是能表达成\(2^{2^k}+1\)(k=0,1,2,...)的素数。
 |
| 邮票上的高斯与正十七边形 |
高斯还写道,他认为能用尺规作图作出的正多边形的边数也必定符合这个条件,但他没有给出证明,详细的证明在1837年由另一位数学家旺策尔给出。他的证明涉及代数中的所谓“分圆域”和“域扩张”的理论,这又是一个用代数方法解决几何问题的例子。根据他们的结论,正七边形自然不能用尺规作图作出。然而对于能作出的正多边形,他们的理论并没有给出实际的作图方法。
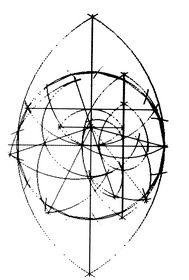 |
| 正十七边形的尺规作图 |
在这些能用尺规作图画出来的正多边形中,边数为费马素数的正多边形自然是最基本的。直到现在,我们只发现了5个费马素数,分别是3,5,17,257,65 537。正三角形和正五边形的作法,早在古希腊的《几何原本》中就有记载。高斯给出了正十七边形的作法,而对于另外两个费马素数,不怕麻烦的数学家也给出了对应的正多边形的作图方法。据说其中正65 537边形作法的手稿有整整200页,可见这些作图方法多么繁复。
高斯关于正十七边形的定理其实有着更深远的意义。当时19岁的高斯在大学里对数学和文学都很感兴趣,而他在尺规作图上的突破激发了他对数学的兴趣,使他坚定了投身数学的意向。他本人也很喜欢这个定理,甚至希望在自己的墓碑上刻上一个正十七边形。高斯的数学生涯硕果累累,而对数学的兴趣,正是高斯打开数学之门的钥匙。