请你在一个长方体容器中灌进一些有颜色的水（便于观察），固定容器底面的一边，将容器慢慢倾斜，但不能使水从容器中倒出。随着容器倾斜程度的不同，你会发现水的各个表面的图形的形状和大小也随之变化。你能通过仔细观察，找出这些图形的形状和大小之间所存在的规律吗？

首先，让容器直立在桌面上，并设容器底面长方形为ABCD，如图1所示。这时，水的前侧面BCFE是长方形，水的形状可看成以BCFE为底，以CD为高的长方体，所以，水的体积等于BCFE的面积与CD的乘积。

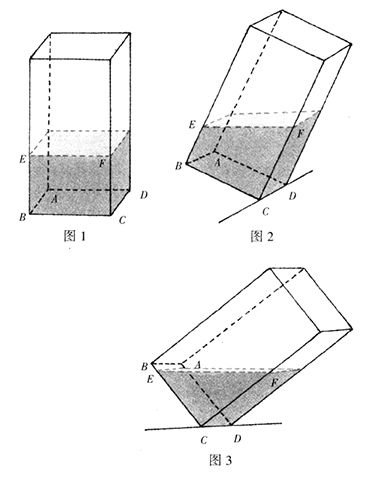接着，固定容器底面ABCD的边CD，将容器慢慢倾斜到图2所示的位置，这时水的前侧面BCFE为梯形，设梯形的上、下底分别为BE=a，CF=b，那么a+b是一个定值，而且，随你怎样倾斜，只要水的前侧面是梯形，a+b总固定不变。同时，左侧的a减少时，右侧的b就增加，a减少多少，b就增加多少。你知道这是为什么？

其实，水的形状可以看成以梯形BCFE为底、CD为高的四棱柱，因而水的体积又等于BCFE的面积与CD的乘积，但是，水的体积和CD的长度没有变，于是前侧面梯形的面积也不变，仍等于图1中前侧面长方形的面积。

我们知道梯形面积等于它的上、下底的和与高的乘积的一半，这里，梯形BCFE的高BC固定，所以上、下底之和a+b就固定不变。

继续倾斜容器到图3所示的位置，这时水的前侧面为三角形ECF，水的形状可看成以三角形ECF为底、CD为高的三棱柱，而水的体积和CD都没有变，所以，水的前侧面面积也没变，仍与图1中的长方形BCFE及图2中的梯形BCFE相等。这时如果设CE=c，CF=b，则因三角形ECF的面积=$\frac{1}{2}$×b×c固定，就有b×c固定不变。

现在我们知道了，由图1所示的位置，依次将容器倾斜到图2、图3所示的位置，在这个过程中，水的形状逐渐由长方体变为三棱柱，水的前（后）侧面形状逐渐由长方形变为三角形，水的表面长方形（由上往下看）面积逐渐由小变大。但是，水的体积和水的前（后）侧面面积不变。