在日常生活中，我们经常与A4纸打交道，这种纸的标准尺寸是210毫米×297毫米。算一下它的长宽比：\(\frac{297}{210}\)=\(\frac{99}{70}\thickapprox\)1.414。若取两张A4纸，沿着纸的长边把它们拼在一起，可以得到一张大纸，尺寸是：420毫米×297毫米。再算一下它的长宽比：\(\frac{420}{297}\thickapprox\)1.414。

大纸与小纸的长宽比基本不变，而且都与\(\sqrt{2}\)相当接近。这是否是巧合？事实上，如果一张纸具有理想的长宽比\(\sqrt{2}：1\)，那么它会把自己的长宽比“遗传”给“下一代”。具体来说就是：最初大长方形纸的长宽比为\(\sqrt{2}：1\)，把这样的大纸沿长边对折后得到的小长方形纸长宽比为\(1：\frac{\sqrt{2}}{2}\)，即仍为\(\sqrt{2}：1\)。这样的操作还可以重复多次，A系列纸正是通过这种方式得到的。

在A系列纸中，原始纸称为A0，它的尺寸规格是1189毫米×841毫米。简单计算可得它的面积接近1平方米，而长宽比非常接近\(\sqrt{2}：1\)。把A0纸沿长边对折裁开，于是得到A1纸，其规格为841毫米×594毫米。对A1进行同样的操作，就得到A2纸，其规格为594毫米× 420毫米，以此类推，即可得到A系列型号的纸。

那么选择长宽比为\(\sqrt{2}：1\)的纸在实际中有什么好处呢？简单说来，用具有这种性质的纸张备料没有剩余的碎纸边，可避免浪费，从而降低再生产的成本并提高工效。

我们现在普遍采用的纸的型号除A系列外，还有B系列。对B系列而言，原始纸B0的规格是1456毫米×1030毫米，这是按长宽比\(\sqrt{2}：1\)、面积1.5平方米确定的。对它反复进行对折裁开操作，可依次得到B1、B2等一系列B型号的纸。

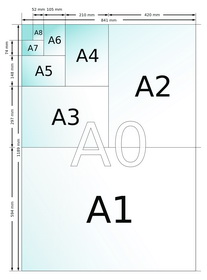A系列纸的尺寸规格