平时，人们说话、办事情，可以区分出有理还是无理，怎么数也会有存理和无理之分呢？说起来倒还有一段有趣的故事哩！

公元前6世纪，古希腊有个数学家叫毕达哥拉斯，他认为，世上的一切都具有整数或者整数之比（分数）那样的性质。比如，所有线段的长度，都能用整数或整数之比来表示；在用力相等的情况下，当琴弦的长度之比为2:3、3:4等整数之比时，各弦就同时发出谐音。总之，毕达哥拉斯的观点是“宇宙万物皆整数”。

然而，事实并非如此。一天，有个学生问毕达哥拉斯，边长为1的正方形的对角线，能不能用整数和整数之比来表示？要明确地回答这个问题就得证明。于是毕达哥拉斯进行了如下的证明：

如图所示，假设边长为1的正方形的对角线可以写成整数或整数之比，那么可令这个比为$\frac{p}{q}$，并且p与q之间没有公约数（当q=1时$\frac{p}{q}$便是整数）。

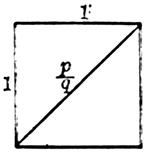根据勾股定理（毕达哥拉斯很早就发现了这个定理），有

${\left( {\frac{p}{q}} \right)^2}{\text{ = }}{1^2} + {1^2}{\text{ = }}2$，

即p²=2q²。

∵2q²是偶数，即p²是偶数，

∴p应是偶数。[p不可能是奇数，因为任一奇数2n+1的平方（2n+1）²=4n²+4n+1必是奇数]

又∵p与q没有公约数，

∴q必是奇数。

p既是偶数，则可设p=2a；

于是p²=4a²=2q²，

即q²=2a²。

这说明q²，是偶数，q也该是偶数；但q同时又是奇数，这就产生了矛盾。因此，边长为1的正方形的对角线的长度，不能用整数或整数之比来表示。这一结果使毕达哥拉斯陷入了困境，也促使人们对数作进一步的认识。

不能用整数或整数之比来表示，并不说明这条对角线的长度不存在。事实上，用勾股定理很容易得出这长度应是“2的算术平方根”，即${\sqrt 2 }$。这样，也就在整数与整数之比之外又发现了一种当时所不知道的新的数。由于希腊人称整数之比为“ratio-nal number”，意思是“成比（ratio）的数”，因此像${\sqrt 2 }$那样的不能写成整数与整数之比的数，就很自然地被称之为“ir-ratio-nal number”，意思是“不能成比的数”。可是，rational这个词有“有理”、“合理”的意思，而“irrational”则有“无理”、“不合理”之意，所以在后人翻译这两个名词的时候也就译成了“有理数”和“无理数”了。

近年来有人提出，应该把“无理数”改称为“不能成比的数”，这虽有道理，但却无此必要。因为一则事情已过百年，习惯了，改了不便；二则“有理数”、“无理数”这些词也实属不错，体现了它的来历不凡，更具有历史性。