在中学教科书中，除了常用对数\(lg x\)外，还有自然对数\(\ln x\)，它表示以\(e\)为底的对数，这里e=2.718 281 828\(\cdots\)为什么把以\(e\)为底的对数称为自然对数呢？

在现代的教科书中，对数函数是按指数函数的反函数来定义的，但历史上并非如此。对数是苏格兰数学家约翰·纳皮尔于1614年首先提出来的。纳皮尔发明的对数可把两个数的乘法运算转换成加法运算，从而大大简化了当时天文、航海等科学领域中遇到的繁杂计算问题。一个满足下列性质的函数

\[y=f(x)，(x>0)；\]

\[f(x_1x_2)=f(x_1)+f(x_2)，f(1)=0.\] 称为一个对数函数。人们在寻求对数函数的过程中发现了下列一个事实：任意给定一个正的常数\(c\)，并在第一象限中考虑双曲线\(y=c/x，(x>0)，\)如图所示。

设\(s\)为任意一个正数，并把图中阴影部分的面积记为\(L_c(s)\)。我们约定，当\(s=1\)时，这个面积为0；当\(s>1\)时，其面积为正；而当\(\)时，其面积为负。在这种约定下，函数\(L_c(s)\)就是一个对数函数。

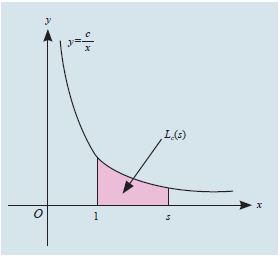第一象限中的双曲线 \(y=\frac{c}{x}\)

苏格兰数学家约翰 纳波尔

现在，我们把\(c=1\)所对应的对数函数记为\(y=L(s)\)。当时有人就把\(L(s)\)称作自然对数，这是因为它是对数函数\(L_c(s)\)中最为简单的对数函数，为了便于计算，还可用它去表示其他对数函数。实际上，早在纳皮尔提出对数的第二年，有人就利用它编制出了对数表，并附录在纳皮尔的书中。但当时人们并不知道什么是数e，也没有“对数函数的底”这个概念。

到了18世纪，欧拉把对数函数与指数函数联系起来，将对数函数看成指数函数的反函数，这时才有了对数函数的底这个概念。欧拉还发现，被人们称作自然对数底的数恰好就是数e。