大家知道，形如\(a\)+\(bi\)的数称为复数，其中\(a\)，\(b\)是实数，而i代表\(\sqrt{-1}\)。复数和我们通常所认识的实数有很大不同，似乎在我们的现实世界中也遇不到这样的数。为什么我们非要引进这样的数不可呢？

中学的数学课本已经告诉我们，当我们解一个二次方程 \[ax^2 + bx + c = 0\] 时，如果\(∆=b^2–4ac<0\)，则方程有一对共轭复数根。不错，引入复数使得\(∆<0\)时也有根了，但此时方程在实数范围内没有根可能更符合实际，人为地引入看不见摸不着的复数根似乎也没有必要。

历史上，复数是在16世纪由意大利数学家卡尔达诺引进的。他引进复数最主要目的是为了求解三次代数方程。为此，我们先看一个例子，考虑三次方程 \[x^3–7x+6=0.\] 容易验证，上述方程有3个实根：\(x\)=1，\(x\)=2和\(x\)=–3。由于三次方程最多有3个不同的根，所以上述3个根就是该方程的全部根。 卡尔达诺当时已经知道形如 \[x^3 + px + q = 0\] 的三次方程的求根公式是 \[x=\sqrt[3]{-\frac{q}{2}+\sqrt{∆}\ }+\sqrt[3]{-\frac{q}{2}-\sqrt{∆}\ }，\] 其中\(∆=(\frac{q}{2})^2+(\frac{p}{3})^3\)。现在，对方程\(x^3 – 7x + 6 = 0\)应用上述求根公式，这时\(p=–7，q=6，∆=-\frac{100}{27}\)。这样，在上面的公式中，就必须处理像\(-3\pm\sqrt{-\frac{100}{27}}\)这样的数，才能最终得到3个实根。

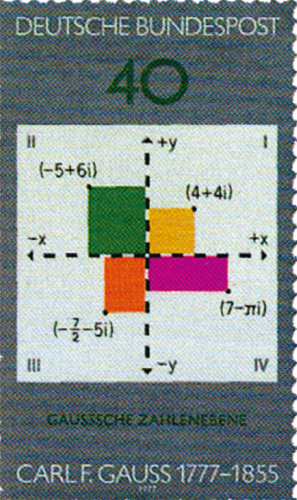邮票上的复平面

卡尔达诺注意到，当∆<0时，为了求得三次方程的根（哪怕是实数根），人们也无法躲过对负数开方的运算，而不得不处理由负数开方所产生的新的数，比如像前面的。这样，卡尔达诺把一类新的数引入了数学。这就是当今我们称之为复数的数。

当时的人把这种数统一写成 \(a+b\sqrt{-1}\)的形式，其中\(a\)与\(b\)是实数。后来，欧拉建议用i来替代\(\sqrt{-1}\)，于是便有了今天复数的表示：\(a\)+\(bi\)。

复数被引入数学之后，不但从此“留下不走了”，而且其用处不断扩大。复数不仅用于解三次或四次方程，还用于三角函数的计算。著名的棣莫佛公式 \[(\cos \theta+i\sin \theta)^n=\cos {n\theta}+i\sin {n\theta}\] 就是一例。在其中取n=2和n=3就可得到三角函数的倍角公式和三倍角公式，并且由此还可得到n倍角公式。有很多实数域中的问题，通过复数域可以简单或巧妙地解决。对此，法国数学家阿达马有一个很恰当的评价：实数域中两个真理之间的最短路径是通过复数域。