我们已经知道了“中国剩余定理”，即“韩信点兵”问题，它是中国古代数学中的一项重大成就，其内容属于数论中的一次同余数组的解法。而这一古老的知识，现在在计算机编码方面也找到了新的用途。

“韩信点兵”问题的答案可以有很多，它们之间都相差105（即3×5×7），但在105之内的解是唯一的。现在我们来简化一下:3个一数余2，5个一数余3，这样的数是多少呢？不难求出，是8，23，38，53，…，它们之间都相差15（即3×5）。而在15之内解是唯一的:8。那么，这样的题目可以编出多少个呢？3个一数，余数可以是0、1、2，共3种；5个一数，余数可以是0、1、2、3、4，共5种，合起来共3×5，即15种。就是说，可以编15个这样的题目，它们的答案各不相同，而且在15之内解又都是唯一的。可见，这15道题的答案正好分别等于1，2，3，…，15。

现在，把这15个数一一填入一个3×5的方格纸的方格内，使得每个数所在的行数是这个数3个一数的余数，所在的列数是这个数5个一数的余数。比如8，是“3个一数余2”，就填在第二行，它又是“5个一数余3”，就填在第三列。

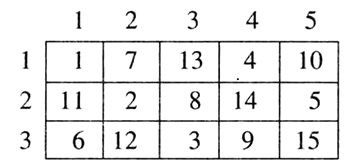任何一台计算机，都有一定的“字长”。字长就是它所能处理的数的最大位数。那么，当我们要利用计算机来处理一个位数超过额定字长的数据时，该怎么办呢?通常的办法是将这个大数用两个小一点的数来表示。最简单的方法是把大数分成两段，如3517，可以分成35和17两个小一点的数。但是这样做，计算机在运算时困难较大，因而一般认为是不可取的。

利用中国剩余定理，可以将一个大数用两个较小的数表示（或编码），并且使计算机运算起来十分方便。我们来看前面说过的3×5的方格纸，8填在第二行、第三列，它可以用2和3来表示；同理15可以用3和5来表示……如果我们的计算机原来只能处理5以内的数，现在就可以处理到15了。而且，这样编码后，运算也十分方便。

比如，在第二列中取一个数2，第三列中取一个数3，它们的积是6，在第一列。而且，第二列中的任何数与第三列中的任何数的积必定在第一列（当积超出15时，可以按前面的方法继续将16，17，…填在3×5的方格中）。

这是什么缘故呢？原来，在同余式理论中，如果

x₁≡x₂(mod5),y₁≡y₂(mod5)

（即x₁和x₂被5除后有相同的余数；y₁和y₂被5除后有相同的余数），那么

x₁y₁≡x₂y₂(mod5),

也就是x₁y₁和x₂y₂被5除以后有相同的余数。利用这个性质就可以证明，与2和3同列（同在一列的数被5除后有相同的余数）的数的积必与6同余，即同在一列。

对行也有相同的结果。

这样一来，计算机在进行大数的运算时就十分方便。例如，我们要做乘法2×6，我们首先对两个数进行编码：

2——（第二行、第二列）；

6——（第三行、第一列）。

可以证明，第二行与第三行中的数的积必在第三行；第二列与第一列中的数的积必在第二列。于是，积可以用3与2表示（或编码）。从表中一查，即可知2×6的积为12。

也就是说，先把两个大数分别表示为两个较小的数（表中的行、列的序号）；然后根据两个行的序号定出两个大数积的行序号，根据两个列的序号定出积的列序号；最后，根据积的行和列的序号在表中就可以查出积的数值，这样，计算机就可以很方便地求出大数的乘积了。

因此，利用中国剩余定理进行计算机编码是非常有用的，我们祖先的智慧进一步地体现在了现代科技中。

关键词：中国剩余定理 同余 编码