为什么在虚数里要采用i作单位
我们知道负数的平方根在实数范围内是没有意义的。譬如-4的平方根在实数范围内就没有意义,因为+2的平方是+4,-2的平方也是+4,不可能找到一个实数它的平方会等于-4的。
这样,我们就引进了虚数。通常习惯,我们把i定作虚数的单位。
虚数的单位为什么要用这个字母i呢?
因为虚数的外文imaginary的第一个字母是i,所以就把i作为虚数单位的符号。
i等于多少呢?它和实数的关系是i2=-1。
 |
为什么不用符号![]() 作为虚数的单位呢?
作为虚数的单位呢?![]() 不是不要字母了吗?
不是不要字母了吗?
这中间也有一个缘故。在代数里![]() =2,
=2,![]() =1,这叫做算术根。我们说正数的正的方根叫做算术根,但
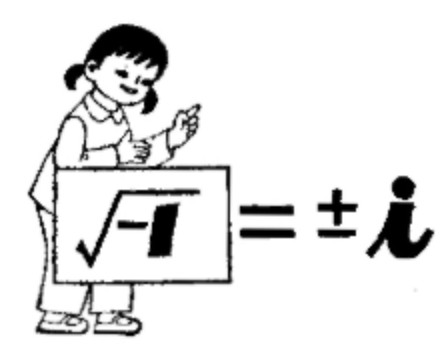
=1,这叫做算术根。我们说正数的正的方根叫做算术根,但![]() 表示的是负数的平方根,这里就不符合算术根的定义。所以严格讲起来,-1的平方根有两个,一个是+i,一个是-i,即
表示的是负数的平方根,这里就不符合算术根的定义。所以严格讲起来,-1的平方根有两个,一个是+i,一个是-i,即![]() =±i。
=±i。
因为![]() 没有象算术根那样规定单值。
没有象算术根那样规定单值。![]() 是可以表示+i或-i的,所以我们要尽量避免
是可以表示+i或-i的,所以我们要尽量避免![]() 这样的写法。
这样的写法。
譬如,在复数范围内解二次方程时,x2=-2,要写x=±![]() i。可不可以写做x=±
i。可不可以写做x=±![]() =±
=±![]() i呢?也是可以的,因为这里正负符号是同时出现的。
i呢?也是可以的,因为这里正负符号是同时出现的。
又如,解方程x2+x+1=0,用公式法
x=![]() =
=![]() 这里正负号也是同时出现的。
这里正负号也是同时出现的。
在正负号不同时出现时,如果说![]() =
=![]() i,这个说法是不妥当的。
i,这个说法是不妥当的。