如果让小球沿着连接\(A\)与\(B\)两点的轨道滚下，在不计摩擦力的情况下，希望它能在最短的时间落到底部，这样的轨道应该做成什么样的形状？

这个问题初看起来一点也不难，似乎这个轨道应当做成直线形，因为两点之间以直线为最短。可是，这个问题并不是要求最短的路线，而是要求最短的时间。要知道：小球下落的时间不仅跟路线的长短有关，而且也跟小球下落的速度有关。如果把轨道的中部向下弯曲，从点\(A\)开始的部分就比直线形轨道更陡，因此，小球沿这部分轨道落下来所获得的速度，一定比在同样长短的直线形轨道上下落所获得的速度大。另外还要注意到一点，倘若把轨道的上半部分做得太陡，那么，下面与点\(B\)连接的部分就会很平坦，因此，小球在轨道的前半部分虽然跑得很快，可是到了后半部分就跑得较慢，到达点\(B\)所用的时间也不一定最短。

雅各布 伯努利（左）与约翰 伯努利在研究数学问题

到底应当把轨道做成什么样的形状呢？意大利物理学家兼天文学家伽利略就曾经考虑过这个问题，他认为这个轨道应当做成圆弧形。可是在半个世纪后的1696年，瑞士数学家约翰·伯努利通过分析证明了结果并非如此，这个轨道应当弯曲成摆线的形状。第二年，牛顿、雅各布·伯努利和莱布尼茨等同时代的大数学家，也都通过各自的计算得出了同样的结论。从这个时候起，摆线就获得了最速降线的名称。

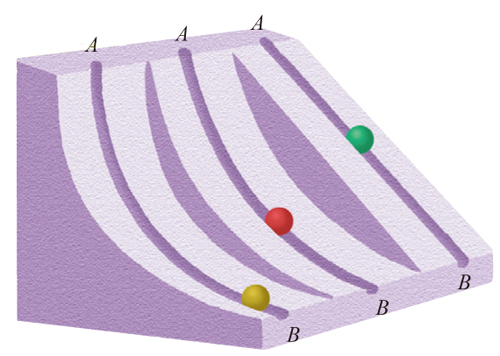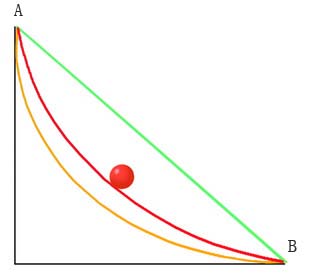小球沿轨道下滑

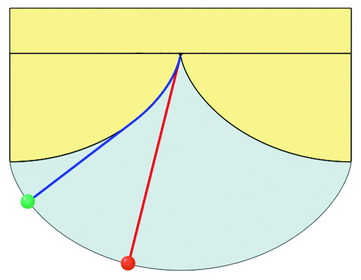
这样的结论确实令人吃惊。同其他任何形状的轨道相比，一个正在滑落的小球沿摆线形轨道滚落下来所需要的时间更短，即使这是一条相对于直线和圆弧来说较长的轨道。最短的路径（直线）并不真正是最快的路线，这确实出人意料。

更令人吃惊的事还在后头。无论从摆线形轨道上的哪个点开始，沿该轨道滑落的小球都会在同一时间到达底部。利用这个原理可以设计出计时很准的机械摆钟。这也是摆线名称的来源。

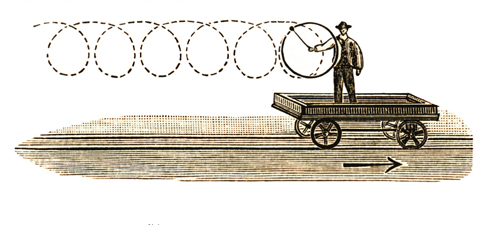一条摆线类曲线——长摆线

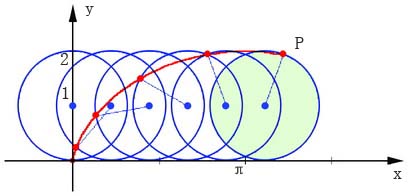摆线的生成过程

小球的摆动轨迹就是摆线

讲了这么多摆线的奇妙性质，那么摆线究竟是怎样的曲线呢？当一个圆在定直线上滚动（而不是滑动）时，该圆周上一个定点所描绘出的曲线，就是“摆线”，又叫作“旋轮线”。

这个问题的解答方法，后来发展为一个新的数学分支——变分学，在数学史上有着重大的作用。