什么叫做区域？直观地说，就是用曲线或者直线划分平面所成的各部分。譬如在平面上画一个圆，把平面分成圆内和圆外两个部分，圆内和圆外就叫做不同的两个区域。在绘制地图时，如果需要把相互相邻的省（或区）着上不同的颜色，我们从绘制地图的经验得知，只要用4种不同的颜色就可以了。但是，在下面的特殊情况下，只需用2种颜色，就可以在相互相邻的区域里着上不同的颜色。

问题是这样的：在平面上有n条直线，一共把平面分成若干区域，现在用黑白两种颜色，要使所有相邻的区域，能着上不同的颜色。

如果给我们一个若干条直线所划分区域的具体图形，用黑白两色按照上述要求进行着色，是不会发生任何困难的。但是，要我们说明当直线是n条时，上述要求的着色一定可能的道理，恐怕就不容易说得清楚了。现在让我们一边作图，一边分析，问题就容易说明了。

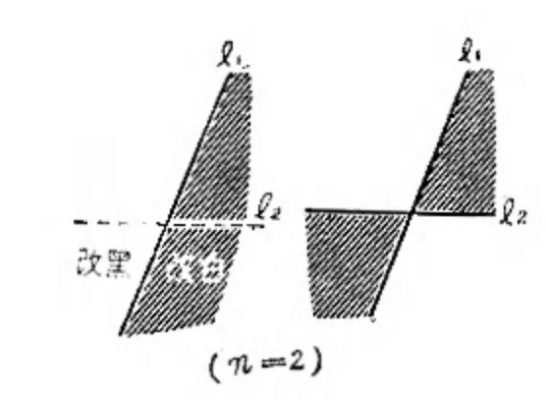
先画上第一条直线l₁，平面被分为两个区域，只需把一边涂上黑色，另一边再涂上白色就可以了。

所以，当n=1时成立。

如果再画上直线l₂，只要在l₂的任何一侧，把所有的区域改变原来的首色，就是把白的改黑，黑的改白就可以了。

所以，当n=2时也成立。

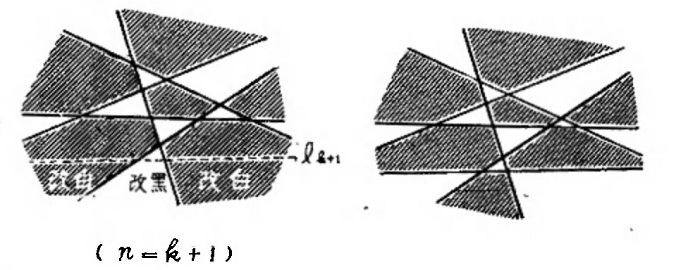
我们依上法画下去，并假定当n=k时仍然成立。就在这个图上，再添上第k+1条直线l_k+1然后把直线l_k+1的一侧所有的区域改变原来的着色，即黑的改白，白的改黑；照这样改变着色以后，就能与直线l_k+1的另一侧所有相邻的区域，具有不同的着色。

而且直线的改变着色那一侧的区域，本来是黑白两色相间的，现在全部改变它们的颜色后，显然仍是黑白两色相间的。

所以，当n=k+1时仍然成立。

因此可以说明，当n是任何自然数时，n条直线划分平面所成的区域，用黑白两色区别着色，是完全可能的。