五角星是大家熟悉而喜爱的图形，下面我们来介绍一种五角星的尺规作图方法。

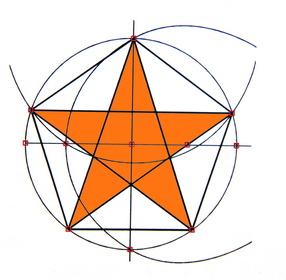五角星的尺规作图

步骤如下：

第一步，画一个圆，作出两条互相垂直的直径\(XY\)与\(AZ\)；

第二步，设圆心为\(O\)，定出\(OY\)的中点\(M\)；

第三步，以\(M\)为圆心，\(MA\)为半径，作圆弧，它与半径\(OX\)交于\(N\)点；

第四步，以\(A\)为圆心，\(AN\)为半径，在圆周上连续截取相等的弧，从而使弦\(AB\)=\(BC\)=\(CD\)=\(DE\)=\(EA\)；

第五步，连接\(AD\)，\(AC\)，\(EB\)，\(EC\)，\(BD\)，此时你将会看到，五角星已经画好了。

现在来证明方法的合理性。设圆的半径为\(R\)，由上述作法可知 \[{AN}^2={AO}^2+{ON}^2={AO}^2+(AM–OM)^2，\] 于是有 \[AN=\sqrt{R^2+(\frac{\sqrt{5}}{2}R-\frac{1}{2}R)^2}=\frac{1}{2}\sqrt{10-2\sqrt{5}}R\] 这也正是圆内接正五边形的边长。以\(AN\)为半径，在圆上截取的五个顶点\(A\)，\(B\)，\(C\)，\(D\)，\(E\)就是圆内接正五边形的顶点。

尺规作图工具（尺上的刻度是用不到的）