圆周率π是一个众所周知的数学常数。π的计算，是古代各大文明都会遇到的问题。

据文献记载，中国在公元前1200年时使用的圆周率π≈3，这就是所谓“周三径一”。

人们认识到用3作为圆周率有较大的误差。西汉末的刘歆曾使用3.1547作圆周率，东汉的张衡则使用了π=\(\sqrt{10}≈3.1622\)，这已经比“周三径一”精确了许多。但这些数值只是一些估计，并非通过数学方法推导出来的。

在中国，对圆周率计算做出重大贡献的首推魏晋时期大数学家刘徽。他在给《九章算术》作注时，创造了计算圆周率的“割圆术”。

刘徽首先指出，“周三径一”实为圆内接正六边形的周长与直径之比，而非真圆周率。他接着指出，正六边形的边长乘以半径再乘以3，就得到圆内接正十二边形的面积；同样道理，将正十二边形的边长乘以半径再乘以6，得到内接正二十四边形的面积；如此下去，“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失也”。而边长可以反复运用勾股定理和开方术求得，刘徽计算了正96边形的边长以及相应186边形的面积，算出π≈157/50=3.14，被称为“徽率”。进一步用其改进算法求得他自己满意的数值π≈3.1416。

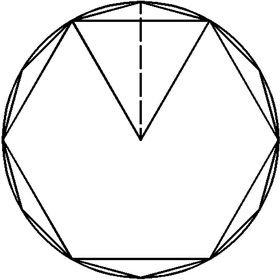刘徽的“割圆术”示意图

用现代的数学语言表示，如果记圆半径为r，内接正n边形的边长为\(S_n\)、面积为\(A_n\)，刘徽给出了如下正多边形面积公式： \[A_{2n}=\frac{1}{2}nS_nr.\]

当\(n\)越来越大，以至于无穷大时，正2\(n\)边形的面积\(A_{2n}\)变成了圆面积\(A\)，正n边形的周长\(n\)\(S_n\)就变成了圆周长\(L\)，这就得到圆面积公式\(A=\frac{1}{2}Lr\)。取\(r\) =1，就得到圆周率的下界估计π=\(A\)>\(A_{2n}\)。为了得到圆周率的上界估计，刘徽注意到圆面积\(A\)与内接正\(n\)边形的面积\(A_{n}\)之差不超过2倍的内接正2\(n\)边形面积和内接正\(n\)边形面积之差\(A_{2n}\)–\(A_{n}\)，因此，有 \[π< A_n+2(A_{2n}–A_n)=2A_{2n}–A_n.\]

这样就得出刘徽计算圆周率的公式: \[A_{2n}< π < 2A_{2n}–A_n.\]

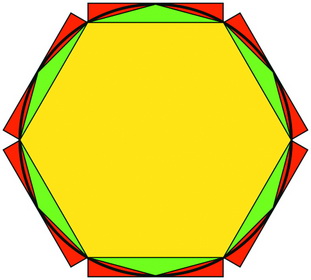刘徽求圆周率上下界示意图

刘徽

刘徽对计算圆周率的贡献在于：他提出的割圆术是计算圆周率π的一般性科学方法，其中蕴含了朴素的极限思想。利用割圆术，只要你掌握了一定计算技能并有足够的毅力，就可以计算出任意精度的圆周率。尽管刘徽不是提出计算π值一般方法的第一人，阿基米德比刘徽要早5个世纪，但刘徽用计算内接正多边形面积的方法具有其特殊的优越性。用正多边形面积逼近圆面积更加直观，更加容易理解。阿基米德要分别计算圆的内接和外切正多边形的周长才能求得π的上下界，而基于面积方法，刘徽仅用了内接正多边形就可求得π的上下界。比较阿基米德的公式 \[\frac{1}{2}nS_n< \pi < \frac{nS_n}{2\sqrt{1-{S_n}^2/4}},\] 我们看到，刘徽的计算公式更简洁，精度更高。刘徽的割圆术确实是一项伟大的创造。

邮票上的刘徽割圆术

200多年后，南北朝时期的伟大数学家祖冲之又进一步计算得到3.141 592 6<π<3.141 592 7，并给出了两个近似分数：约率22/7和密率355/113。祖冲之的圆周率精确到小数点后7位，远远超出了当时世界数学水平，这一精度领先世界长达1000多年，直到15世纪才被阿拉伯数学家卡西超越。一般认为祖冲之所用的方法就是刘徽的割圆术，只要运用割圆术算至正24 576边形，就能达到祖冲之的计算精度。

密率\(355/113=3.141 592 9\cdots\)，前六位和π的真值完全相同，作为π的近似分数极为精确，是分母在16 604以内逼近圆周率的最佳分数。在西方，355/113作为π的近似分数直到1000多年后的1573年才为德国人奥托重新得到。