木匠经常会遇到以下情况：一块长方形的木板，上、下两条对边完好如初，但另外两条对边参差不齐，要用锯子锯整齐，然而手头没有直角尺，怎么办呢？

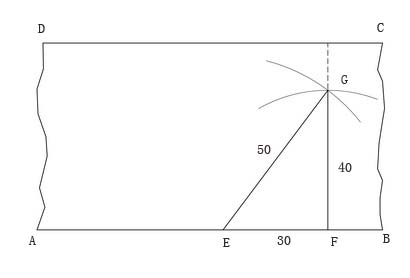用有刻度的用直尺画直角

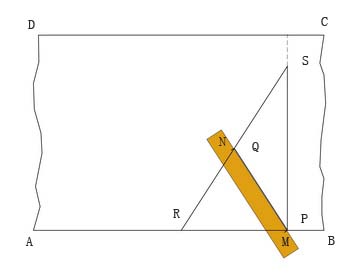用木棒画直角

办法挺简单，只要运用极简单的、古人早已知晓的知识就行。

可利用一把有刻度的直尺，在\(AB\)边上量出相距30厘米的两点\(E\)，\(F\)，然后分别以\(E\)，\(F\)为圆心，以50厘米与40厘米为半径画圆弧，两弧相交于点\(G\)，连接\(FG\)，则\(∠EFG\)必为90°，沿\(FG\)锯下来，就把\(BC\)边修整了。用同样方法可以把\(AD\)边锯好。

这样的做法，原理是一清二楚的，因为\(EF:FG:EG\)=3:4:5，符合“勾三股四弦五”的道理，所以斜边\(EG\)的对角\(∠EFG\)肯定就是直角。

如果条件更差，甚至连有刻度的直尺都没有，也还是有办法解决的。

可以取一根笔直的木棒，用铅笔在棒上点出\(M\)、\(N\)两点。然后把木棒斜放在木板上，使点\(M\)靠着木板的边缘，用铅笔按照\(M\)、\(N\)的位置在木板上记下两点，点\(P\)和点\(Q\)。再把木棒换一个方向，使\(N\)点不动，点\(M\)靠着木板的边，在其位置记下点\(R\)。然后将\(RQ\)延长，在延长线上截取线段\(QS\)=\(MN\)，连接\(PS\)，则\(∠RPS\)=90°。用这个办法即可作出直角，把木板参差不齐的对边锯齐。

刻在大理石上的欧几里得雕像

根据上述作法可知，\(RQ=PQ=QS\)，所以\(△RPQ\)与\(△SPQ\)都是等腰三角形，从而有 \[∠RPS =∠RPQ +∠QPS =∠PRQ +∠QSP.\] 由于\(∠RPS\)、\(∠PRS\)、\(∠RSP\)是\(△RPS\)的三个内角，故其和等于180°，于是立即得出\(∠RPS\) = 90°。

不难看出，此方法的背景是平面几何中的一个定理：“直角三角形中斜边上的中线长度等于斜边长度的一半”，不过是将它变通处理、灵活运用而已。