夜空清澈，群星争辉，闪烁的繁星眨着调皮的眼睛向人们微笑着，仿佛在说：“遥远的地球的主人，你们能知道我们之间的距离吗？”想知道天文学上如何测量恒星的距离，就得先了解一下地面上测定物体距离的一种方法。

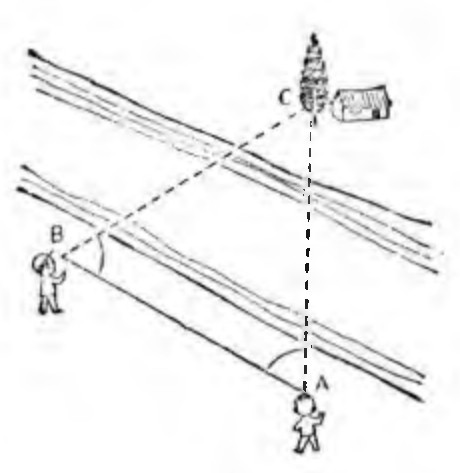
进行大地测暈和一般地形测暈时，往往由于相距过远，以及山、川、河、湖等障碍，而不能用直接方法测定远处一个无法接近的物体的距离。遇到这种情况，测量队常常应用三角方法测量远方目标的距离。例如，要测定位于大河对岸C点这棵树的距离，我们可以在这边的河岸上选择一条足够长的基线（图中直线AB)，当我们从基线两头看对岸大树时，它们的方向将是不同的，其角度可用测角仪器，如经纬仪测出，也就是测定图中的A角和B角，从量得的两个角度和基线的长度，应用正弦定理，通过简单运算便可求得大树与基线任何一端的距离。利用三角测量法时，基线必须选得足够长，如果两个端点A与B靠得太近，尽管分别在A点和B点观测目标C，则犹如在同一处观测一样，测不出方向的变化。因此，测量的目标离我们越远，所选的基线应该越长。

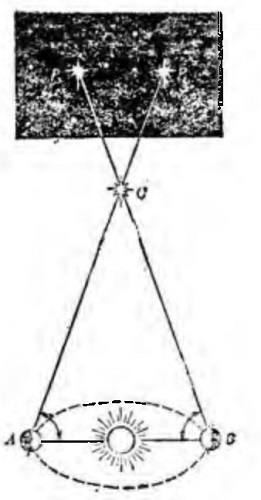
上面所说的方法，也正是测量恒星距离的一种基本方法。不过，恒星离我们都十分遥远，要用这方法测量它们的距离，需要有一条非常长的基线，怎样得到这样的基线呢？天文学家巧妙地利用了地球绕太阳作周年运动的自然规律，当地球位于A的位置时，恒星C好象在遥远的星空背景上的P1处，用望远镜观测这颗星，记录这颗星在星空背景上的位置；过了半年，由于地球的公转运动已把人们带到了地球运动轨道的另一端B处，这颗星又好象在“天幕”上的P2处，再一次测定该星的位置。日地平均距离约1.5亿公里，地球上的人们在半年内移动约等于地球轨道直径的距离，约3亿公里，把这个距离作为一条基线，这样再用上面所说的方法，就能算出这颗星的距离。这种方法早在四百多年前哥白尼就曾经作了尝试，他在相隔6个月的时间内两次测定过同一颗恒星的方位，企图定出这颗恒星的距离。然而由于哥白尼用的仪器不够精密，没有得到成功。到了1833年人们首次观测到恒星一年间在天空背景中兜了一个很小的圈子，这个圈子就象在二十公里以外地方来看一枚5分硬币。但是，后来人们终于成功地用三角测量法定出了恒星的距离。到目前为止，已经用这种方法测定了约10000颗恒星的距离。对于那些距离更远的恒星，即使地球的公转运动所提供的最长的基线也显得太短了，所以我们还必须寻找其他方法。

在日常生活中，大家都有这样的体会：一盏明亮的灯，放得离我们近一些，看起来就更亮些，放得离我们远一些，看起来就暗一些。对恒星也是这徉，离我们近的恒星看起来亮，远的看起来就暗，所以说，平时所看到的星星的亮度，并不是星星的真亮度，我们称之为“视亮度”，它决定于星星的真亮度和它们离我们的距离。测出了恒星的视亮度以后，如果能设法知道恒星的真亮度，就可以计算出恒星的距离了。

怎样才能知道恒星的真亮度呢？这就要利用恒星的光谱了。恒星的光谱好比是“无字天书”。天文学家们发现，在恒星的光谱中，两根不同谱线的相对强度同恒星的真亮度之间有一定的关系，因此只要测量出恒星光谱中不同谱线的相对强度，就可推算出恒星的真亮度，从而推算出恒星的距离来。利用这种方法，现已测量了几万颗恒星的距离。

在天空中还有一种特别的星星，它们的亮度准确地发生着周期变化，这种星称为造父变星。天文学家们发现，造父变星的亮度变化周期和它的真亮度之间有一种奇妙的关系造父变星的真亮度越大，变化周期就越长，这样我们就可以通过观测造父变星的亮度变化周期来求得它的真亮度，然后也就可以求出它的距离了。对于河外星系内的造父变星也能观测到，它们好象是太空中孤岛上特殊的灯塔，以变幻着的光芒为信号向天文工作者暗示孤岛的距离，由于造父变星对天文测距的贡献，被誉为“量天尺”。

测量恒星距离，除了以上各种方法以外，还可以根据一些高光度的天体，如新星、超新星和球状星团等的绝对星等的方法来测量恒星和河外星云的距离。由于科学技术的不断发展，今后可能有更为准确的方法来测量出离我们更远的，更多的星星的距离。