暴风雨过去了，一支巡回医疗队来到河边，那知木桥已被洪水冲断，怎么办呢？正在焦急的时候，忽然看见一条小船向这边驶来。

“啊，太好啦！村里两个少先队员来接我们啦！”大家高兴极了。

可是，这条船实在太小，它只能承载两个孩子或者一个大人。

“怎样才能全部渡到对岸去呢？”大家都在沉思着。

聪明机智的少先队员，很快想出了渡河方案，巧妙地把大家全都渡到对岸。是怎样一个方案呢？

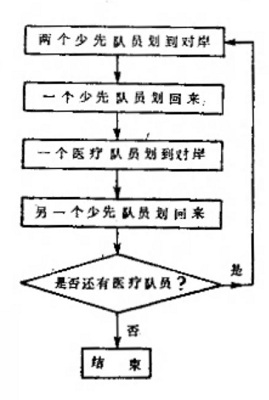
首先，两个少先队员把船划到对岸。

接着，他们之中一个留在对岸，另一个划回来。

这个少先队员上岸，一个医疗队员划过去。

医疗队员上岸，留在对岸的少先队员划回来。

这时，一个医疗队员已到对岸，而两个少先队员却都回到这边来。整个过程这样重复下去，直到每一个医疗队员全都渡过河去为止。

这里渡河的程序是何等重要，先怎样，后怎样，再怎样，必须按一定的次序。为了清楚明白地表示渡河程序，我们把它画成一种带有箭头的框图。

这种框图也叫流向图，在用电子计算机解题时很有用。电子计算机自己不会思考，需要人们去指挥它。用电子计算机解某个实际问题，先要把实际问题归纳为数学问题，再选用适当的计算方法然后画出流向图，表示先算什么，后算什么，再算什么。根据流向图，就可以用电子计算机能懂得的特别语言——算法语言，编写计算程序，在纸带上打孔，输入计算机。这样，电子计算机就会按照你的命令进行运算，并把计算结果打印在纸上。

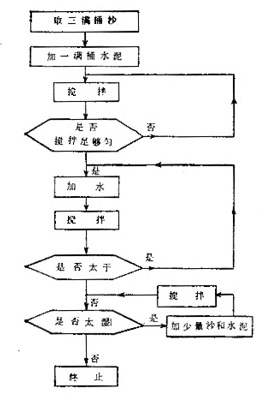流向图的本身是十分复杂的。左面是一个生产上最简单的流向图——搅拌混凝土的流向图。

在渡河的流向图里有一个尖角的框格，在搅拌混凝土的流向图里有三个尖角框格，它们都是问句，有两个“分支”从那里出来，一个“是”，一个“否”。这是因为计算机建立在“是”或“否”的系统上，回答“也许”是不允许的。按照回答的“是”或“否”，沿着各自的“回答”继续做下去，直到整个过程终止。

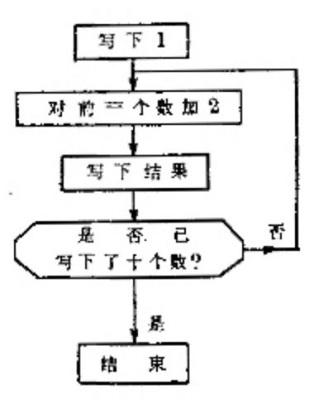
想一想：如果按一张象前面那样的流向图计算，将得到怎样的数集？