五角星是大家很熟悉的一种图形。由于它对称、美观，因而常被用来组成各种图案。这里向大家介绍一种正五角星的精确绘制方法，具体步骤如下：

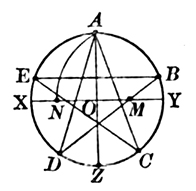
（1）作一个圆，设它的圆心为0。

（2）作圆0的两条互相垂直的直径AZ，XY。

（3）取OY的中点M。

（4）以M为圆心，MA为半径，作圆弧和半径OX交于N。

（5）以A为圆心，AN为半径，在圆O上连续截取等弧，使弦

AB=BC=CD=DE=AN，

（6）连接AD，AC，EB，EC，BD。五角星就画成了。

上述画五角星的方法是精确的。这可以作如下证明：

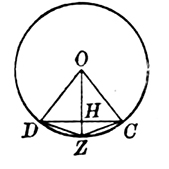设圆O半径为R，DZ=ZC=a₁₀为圆内接正十边形的一边，则DC=a₅是圆内接正五边形的一边。由初中数学课本已经知道

${a_{10}} = \frac{1}{2}\left( {\sqrt 5 - 1} \right)R$，

这样，利用勾股定理就可求得等腰三角形的面积

${S_{\vartriangle ODZ}} = \frac{1}{8}\sqrt {10 - 2\sqrt 5 } {R^2}$。

又${S_{\vartriangle ODZ}} = \frac{1}{2}DH \cdot OZ$，

$DH{\text{ = }}2{S_{\vartriangle ODZ}} \div R = \frac{1}{4}\sqrt {10 - 2\sqrt 5 } R$，

所以${a_5} = 2DH = \frac{1}{2}\sqrt {10 - 2\sqrt 5 } R$。

而由上述五角星的作法知

AN²=AO²+ON²=AO²+（AM-OM）²，

$\eqalign{ & N = \sqrt {{R^2} + {{\left( {\frac{{\sqrt 5 }}{2}R - \frac{1}{2}R} \right)}^2}} \cr & = \frac{1}{2}\sqrt {10 - 2\sqrt 5 } R \cr} $。

即AN=a₅。

圆内接正多边形并不都能用尺规精确作图。除正五边形外，正三角形，正十五边形，以及由它们直接得出的那些边数为2ⁿ，2ⁿ×3，2ⁿ×5，2ⁿ×l5（n是正整数）的正多边形的几何作图在2000多年前的欧几里得时代就已经知道了。但在以后的近2000年间，人们一直没有发现新的可以使用圆规和直尺作图的正多边形。一直到18世纪末，高斯取得了突破，首先作出了正十七边形。高斯还断言：一个正n边形，当且仅当n=2^mP₁·P₁…P_v时，才可用圆规和直尺作图。这里…，分别是形为${2^{{2^k}}} + 1$的不同质数，而m是任意的正整数或0。这一断言的充分和必要性分别为高斯本人和另一个数学家所证明。