整数和偶数一样多吗?许多同学会不假思索地回答：“不！不一样多！因为偶数只是整数的一部分。”或许有少数同学会对这个回答表示怀疑，没有把握地说道：“可能一样多吧，整数可以和偶数一一对应呢。”其中一位同学还在黑板上写下整数和偶数间的一个一一对应：

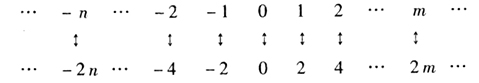两种不同的意见究竟谁是谁非呢？

上述问题的实质是比较整数集合与偶数集合的大小。比较两个有限集合的大小较容易，而对无限集合，什么是它们的“大小”，又如何比较“大小”呢？

对有限集合，集合中元素的个数确定了集合的大小，有那些与我们日常经验非常吻合的判别集合大小的准则，例如，（1）部分小于整体（用集合论的话说，真子集合比全集合小）；（2）如果两个集合间可以建立一一对应，它们是一样大的。上面两种不同的回答正是把这两个准则简单地推广到无限集合。

其实，准则（2）是非常本质的。大家想一想，谁见过抽象的“3”?大家见过的是“3只狗的集合”、“3个人的集合”、“3本书的集合”等等，通过对这些集合的观察，找出它们的共同性而获得“3”这个抽象的概念。为什么这些集合有“3”的共同性，而“4个人的集合”没有这一性质呢？关键是所有这些有“3”的共同性的集合间都能够建立一一对应:3个人牵3只狗，“3个人的集合”与“3只狗的集合”建立了一一对应；3个人读3本书，“3个人的集合”又与“3本书的集合”建立了一一对应。

把这种思维方式推广到无限集合上，我们就可以建立无限集合“大小”的理论——如果两个集合（有限或无限）间可以建立一一对应，就说这两个集合具有相同的基数；如果一个集合可以一一对应于另一个集合的一个子集合，就说第一个集合的基数不大于第二个集合的基数。于是就有了“基数”这样一个抽象的概念，并且可以比较基数的大小。基数是有限集合的元素个数概念的推广。

按这样的定义，最“小”的无限集合是自然数集合，因为如果一个集合是无限的，每次从这个集合中取出一个元素后，集合里总存在没有被取出的元素，于是取元素的过程可以永远继续下去，从而建立了自然数集合与这个无限集合的一个子集合的一一对应。数学上约定用希伯来字母ℵ （读作“阿列夫”）带下标来代表无限集合的基数，并且把自然数集合的基数记为₀。

回到开头的问题，大家也许已经判断出，整数集合和偶数集合具有相同的基数，从而是一样“大”的，即整数和偶数一样“多”。事实上，这两个集合的基数都是ℵ₀——我们只要把整数集合排成一串0，1，-1，2，-2，3，-3，…，整数无一例外地排上了队，于是就建立了自然数集合与整数集合的一一对应。还可以证明，有理数集合的基数也是ℵ₀，大家不妨想想看如何给有理数排个队，以建立自然数集合与有理数集合的一一对应。当然，确实存在基数不是ℵ₀的集合，在下一篇中我们将证明实数集合就是这样的例子。

大家已经看到，尽管无限基数是有限数的推广，但无限基数的某些性质与有限数差异很大。例如，一个无限集合可以与它的真子集合有相同的基数。因此，对有限数自然成立的结论，不能想当然地推广到无限基数。

关键词：整数 偶数 集合 基数